【高専受験生必見!】高専数学の傾向と対策を紹介！

飛高専塾 岐阜駅前校の渡会です。　
今回は高専入試の数学で高得点を取るためのポイントをまとめました。
高専を志望している方の参考になれば幸いです。

目次
１高専数学の難易度
２高専数学の構成
３各大問の傾向
４高専数学の対策

１高専数学の難易度

難易度の参考に岐阜高専の合格者の平均点が公表されているので紹介します。
以下の表をご覧ください。

年度により変化はありますが、全体の傾向としては理科・数学の点数が低く、英語・国語の点数が高くなっています。
高専入試では数学と理科の難易度が高く設定されています。
特に数学は見たことがない問題や思考力を試される問題が出題されることもあります。

しかし、高専の数学がすべて難しい問題という訳ではありません。
むしろ割合としては基本的な問題の方が多いのです。
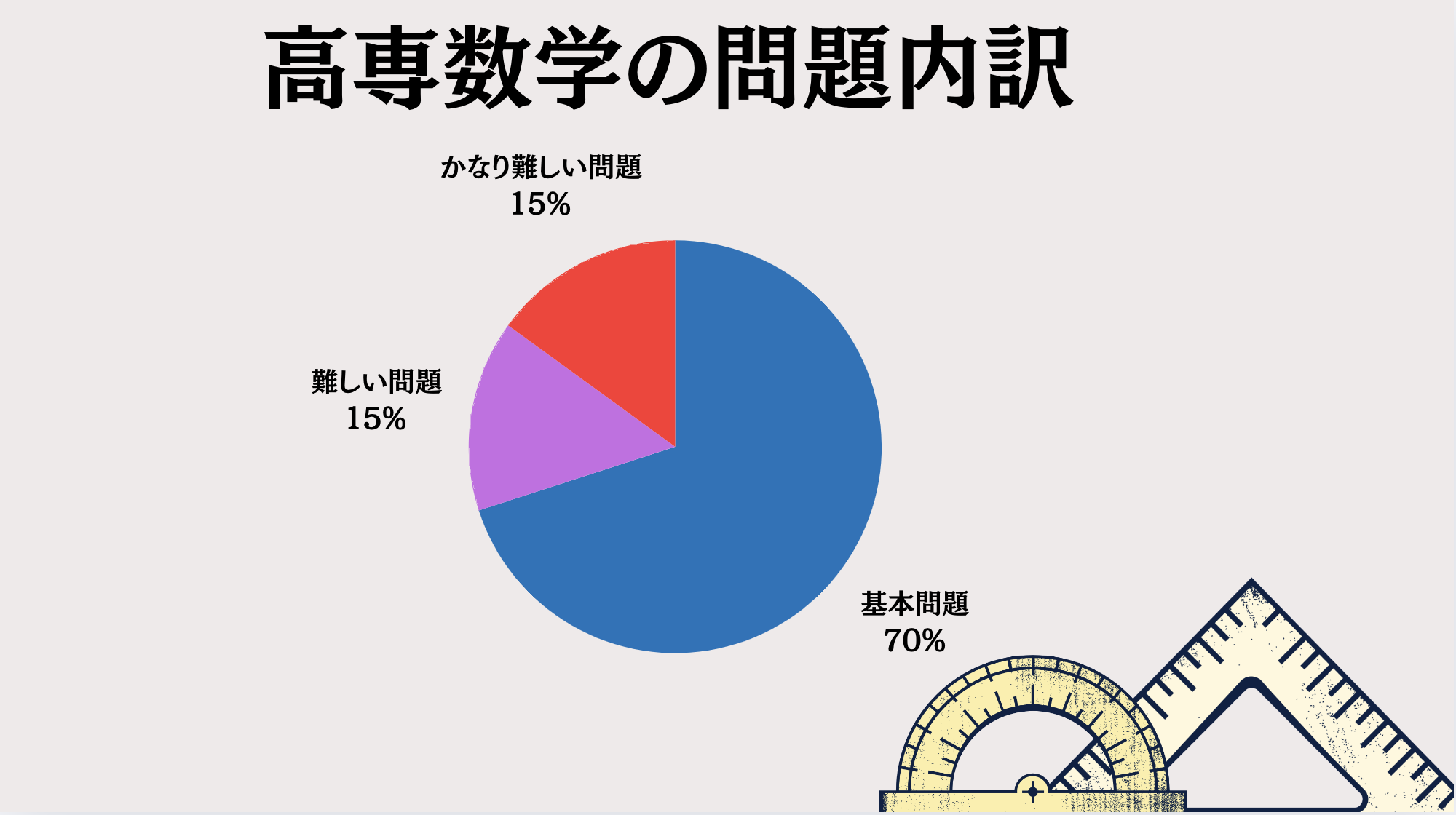
※基本的な問題とは特別な知識や発想を必要としない、入試でよく出題されるふつうの問題という意味です。こうした問題がしっかり解けるようになるのもある程度勉強が必要です。

高専数学は
7割が基本問題
1.5割が少し難しい問題
1.5割がかなり難しい問題

といった感じだと思います。

高専数学は難しそうな印象を受けるかもしれませんが、基本問題が確実に解ければ７割は得点できるはずです。

高専入試の数学は難しい問題を解かなければいけない訳ではなく、基礎～標準レベルの問題を確実に解くことが大切です。

２高専数学の構成

高専の入試数学は４つの大問で構成されています。
大問１は小問集合、大問２～大問４で関数、図形、規則性の問題などが出題されます。

大問１では小問が８個で配点は４０点、大問２～大問４は小問がいくつか出題され配点はそれぞれ２０点です。

大問１は比較的解きやすい問題が多く、大問２～大問４は後半の小問になるにつれ難しくなっていきます。

そのため大問１と大問２～大問４の前半の問題を解くことができれば７～８割くらいの点数になります。

大問１で４０点取り、残りの６０点は半分しか出来なくても全部で７０点というのが基本の作戦です。

３各大問の傾向

ここからは各大問の特徴を紹介します。　

高専数学紹介|小問集合

小問集合は普通の計算問題や二次方程式、変化の割合、確率、データ、図形の角度や面積を求める問題などから約８問出題されます。
公立高校入試の小問よりは難しいですが、高専数学の中では解きやすい問題が多く、問題の傾向も過去問と似たものが多いので、対策はしやすいです。
ただし計算が細かい問題もあり、時々難しい問題も出題されるので、満点を取るのは簡単ではないと思います。

対策は日頃から問題集に載っている問題を丁寧に解いていくことです。
いろいろな単元から出題されるので、全単元の基礎を身に付けておかなくてはなりません。
過去問とほとんど同じ問題が出されることもよくあるので、過去問の問題はすべてできるようにしておきましょう。

大問１だけで配点が４０点あるので、ここを全問正解することが数学で高得点を取るコツです。
多少時間がかかっても、ミスなく正しい答えを求めることを意識しましょう。

高専数学紹介|関数の問題

関数は２次関数が出題されることが多いです。
目新しい問題設定になっていることは少ないので、典型問題の解法が身に付いていればある程度解けると思います。

前半は関数の式や交点の座標を求める問題が出題されます。
このあたりは基本問題なので必ず解けるようにしましょう。

後半の小問は難しい事もありますが、特別な発想などは必要なく、論理的に考えればできる問題です。

中学で学習する二次関数の問題はパターンが決まっていますが、高専の関数もよくある題材です。
対策として、まずは問題集で二次関数の問題を一通り解いて解法を学びましょう。
その後過去問を解いてみて、前半の問題が出来なければ基本的な解法が理解できていないので、すぐに解決しましょう。
後半の問題は初めは難しく感じても、重要な解法を使う問題ばかりです。
よく解答を読んで自分で答えが求められるようになるまで繰り返し解いてみましょう。

二次関数は問題集や過去問で学んだ解法が次に生かしやすい単元です。
ひとつひとつの問題を確実に身に付けていきましょう。

高専数学紹介|図形の問題

高専数学では図形問題が最も難しいことが多いです。
合同や相似、円の知識や三平方の定理など図形の解法を総動員して、辺の長さや図形の面積、体積などを求めます。

前半は素直な問題のことが多いので、しっかり解きましょう。
後半からは発想が必要な問題が多くかなり難しいと思います。
問題によっては試験時間内に完答するのがほとんど不可能な場合もあります。

実際の試験では後半の問題で時間がかかりそうなら、飛ばして次の問題に進んだ方がいいでしょう。本番で最後まで解答できる人は少ないと思います。

しかし普段の学習では答えを見ながらでもいいので、最後の問題までしっかり考えてください。
難しい問題であっても自分で考えて理解しようとすることで思考力がついていきます。

高専数学紹介|規則性の問題

規則性に関する問題などが出題されます。
その時々でいろいろな問題設定の出題がされ、与えられた条件からその場で考えて答えを出さなければいけません。
問題を正しく読み取る読解力が求められます。

一見難しいように見えますが、問題の設定が理解できれば設問自体はそれほど難しくないように感じます。

問題集などで対策することは難しい範囲で、過去問などで類題を解くことが一番の対策になります。
公立入試や私立高校の入試にも同じ系統の問題があるので、そうした問題で練習することもできます。
実際の試験では初見の問題を解くことになりますが、過去問などでいろいろな問題を解いて経験を積むことは大切です。

難問が出されることは少ないので、見たことがない感じの問題でも、問題をよく読めば必ず解けるはずだという気持ちで解きましょう。

４高専数学の対策

高専を目指して学習する際のポイントを紹介します。

高専数学対策|①先取学習をしよう

高専入試では二次関数や相似、三平方など中学三年生の範囲が出題の中心であることが特徴です。
これらの単元を学習しなければ過去問を解くことができませんが、学校で勉強するのを待っていたら手遅れになります。
過去問演習に十分な時間を取るために、早めに中学の全単元を一通り終わらせましょう。
目安としては高専入試の３か月くらい前に中学の全範囲を学習し終え、過去問に入っていけるとよいでしょう。

高専数学対策|②難しめの問題集を使用しよう

学校のワークだけでは対策としては不十分です。
例えば関数の頻出問題に図形の面積を二等分する直線の式を求める問題がありますが、こうした問題は通常の問題集にはあまり掲載されていません。
レベルの高い問題が十分な量掲載されている問題集を活用しましょう。
使用する教材によって学習効率は大きく変わってくるので、高専のレベルに合った教材を使用することが大切です。
　

高専数学対策|③出来るだけ多くの過去問を解こう

高専対策として過去問演習は非常に有益です。
古い問題もそれほど傾向は変わっていないので、出来るだけ多くの過去問を解きましょう。

「過去問で弱点となる分野を発見→その分野を問題集で演習」を繰り返し、精度を上げていくことが受験勉強の基本の流れです。

過去問を解く際は必ず時間を測って解きましょう。
試験時間は意外と短いので全問しっかり考えることは難しいことがあります。
その場合分からない問題に見切りをつけなければいけませんが、時間を測って過去問を解くことで、その判断力が養われます。

また一度解いた問題でも、間違えた問題は完全に理解できるまで繰り返し解いてください。
大問の最後の問題など難しい問題も、できるだけ自分でしっかりと考えて、解き方を理解できるようにしましょう。
解けない問題を解けるようにすることで学力が向上します。

今回は高専入試の数学の傾向と対策について説明しました。
受験生の皆様の参考になれば幸いです。

詳しい入試対策については飛高専塾 岐阜駅前校までご相談ください。
少人数での手厚い指導で、合格までしっかりとサポートします。
お気軽にお問合せください。
問い合わせはこちらから
飛高専塾　岐阜駅前校はこちら