2025.10.01
【受験生必見】国立高専で勝つための”数学対策”

飛高専塾 広島駅前本校 吉川先生
勉強が苦手な生徒でも分かりやすいよう"仕組みを徹底的に言語化"して伝えます! 問題の根本を理解することで、応用問題にも対応できる力を身につけて、本質的な学力向上が図れる指導を意識しています。 また、生徒一人ひとりとコミニュケーションを積極的に取りながら、一人ひとりの生徒と二人三脚で勉強に向き合い、『苦手を得意に』をモットーにご指導いたします。
高専合格を目指すならまずはここから!
飛高専塾の高専入試特別講座に挑戦!!
初めまして!
今回は国立高専を受験する新受験生に向けて高専入試の最難関といっても過言ではない、「高専入試 数学」でどのようにして点数を取るのか?
について、飛高専塾のよっしー先生が詳しくご紹介いたします!!
高専合格への数学対策/高専入試の傾向を知ろう

まず、なぜ高専入試の数学が重要というと、やはり理系の学校として、理科・数学の難易度が高い傾向にあります!
だからこそ、正しい対策で点数を取れるようにすることで他受験生に大きな差をつけることが可能になります!
高専入試数学の傾向①傾斜配点がかかっている
高専数学が最も重要視される理由は高専によって数学に傾斜配点があることです!!
実は国立高専の試験問題は統一されていますが、その配分は各高専によってバラバラになっています!
そして、傾斜配点をかけている高専においては必ず数学の比重が高くなっているといえるのです。
数学に傾斜配点がある高専
| 数学の傾斜配点がある高専 | |
|---|---|
| 2倍の高専 | 徳山高専 函館高専 釧路高専 苫小牧高専 旭川高専 長岡高専 長野高専 八戸高専 松江高専 津山高専 阿南高専 新居浜高専 沖縄高専 仙台高専 東京高専 神戸高専 鹿児島高専 |
| 1.6倍の高専 | 北九州高専 |
| 1.5倍の高専 | 明石高専 茨城高専 沼津高専 久留米高専 熊本高専 舞鶴高専 群馬高専 鈴鹿高専 大阪高専 |
上記のような高専は数学に傾斜配点がかけられています!
さらに、数学に傾斜配点がかかっている高専は、当日点と内申点の比率で見たとき、当日点の割合が70%を超えてくることが多くなりますので、より学力入試で点数を取ることに向けた準備が必要です!
数学に傾斜配点がない高専
| 数学の傾斜配点がない高専 | |
|---|---|
| 5科目受験 | 福島高専 一関高専 富山高専 豊田高専 奈良高専 米子高専 宇部高専 香川高専 大分高専 佐世保高専 呉高専 |
| 4科目受験 | 岐阜高専 和歌山高専 秋田高専 石川高専 都城高専 |
これらの高専では学力入試において傾斜配点がかけられていません。
ただ、それでも内申の比率が当日点より高く設定されている高専はないので、
当日でコケないための対策はしっかりとしていく必要性があります。
高専入試数学の傾向②問題ごとの配点に差がない
高専数学で正しい対策が必要な2つ目の理由が「問題ごとの配点に差がない。」ことです
どういうことかというと、高専入試に出題されているどの問題も難易度に関係なく、配点が設定されています!!
だからこそ、問題ごとの戦略性が非常に重要になってきます。
比較的難易度が優しい問題で確実に正解しきることが「高専に落ちないための最善」です!
難易度が高いと言われる高専入試の数学において、まずやるべきことは難しい問題を解く力を身につけるのではなく、
「確実に解ける問題でミスをしない」が重要になるということです!
ただ、比較的難易度の優しい問題を解いたとしても、当日点で75点を超えるのは難しくなってきます!
さらに、偏差値が高い高専、傾斜配点がかかっている高専に合格したいのであれば、まず80点以上を取ることが理想となります。
したがって、応用問題と呼ばれる難易度が高い問題も短い時間で正解するための力を養う必要性があるのです!
初見問題への対応力、応用力を身につけるための勉強法は特別講座で知ろう!
飛高専塾が主催している高専入試対策特別講座では、50分の中で数学などを解ききるために受験生としてどのような勉強をするべきかを徹底解説しています!
詳細は下記のバナーから確認!!
高専合格への数学対策/高専入試の出題内容を知ろう

上記で記載しているとおり、高専入試の数学は問題ごとの配点に大きな差がありません。
だからこそ、どのような大問が出題されて、どこを優先的に正解していくべきなのかを決めておく必要性があります。
ですので、ここからはそれぞれの大問に何が出題されるのかを説明いたします!
高専入試(数学)の出題傾向/大問1(小問集合)
まず、高専入試の数学は大問が1~4の下記のような内容で構成されています!
| 出題内容 | 配点 | |
|---|---|---|
| 大問1 | 小問集合(8問) | 40点 |
| 大問2 | 関数、方程式、図形、規則性のいずれか | 20点 |
| 大問3 | 関数、方程式、図形、規則性のいずれか | 20点 |
| 大問4 | 関数、方程式、図形、規則性のいずれか | 20点 |
上記からもわかる通り、大問1は小問集合でありながら、最も配点比率が高い問題になっています。
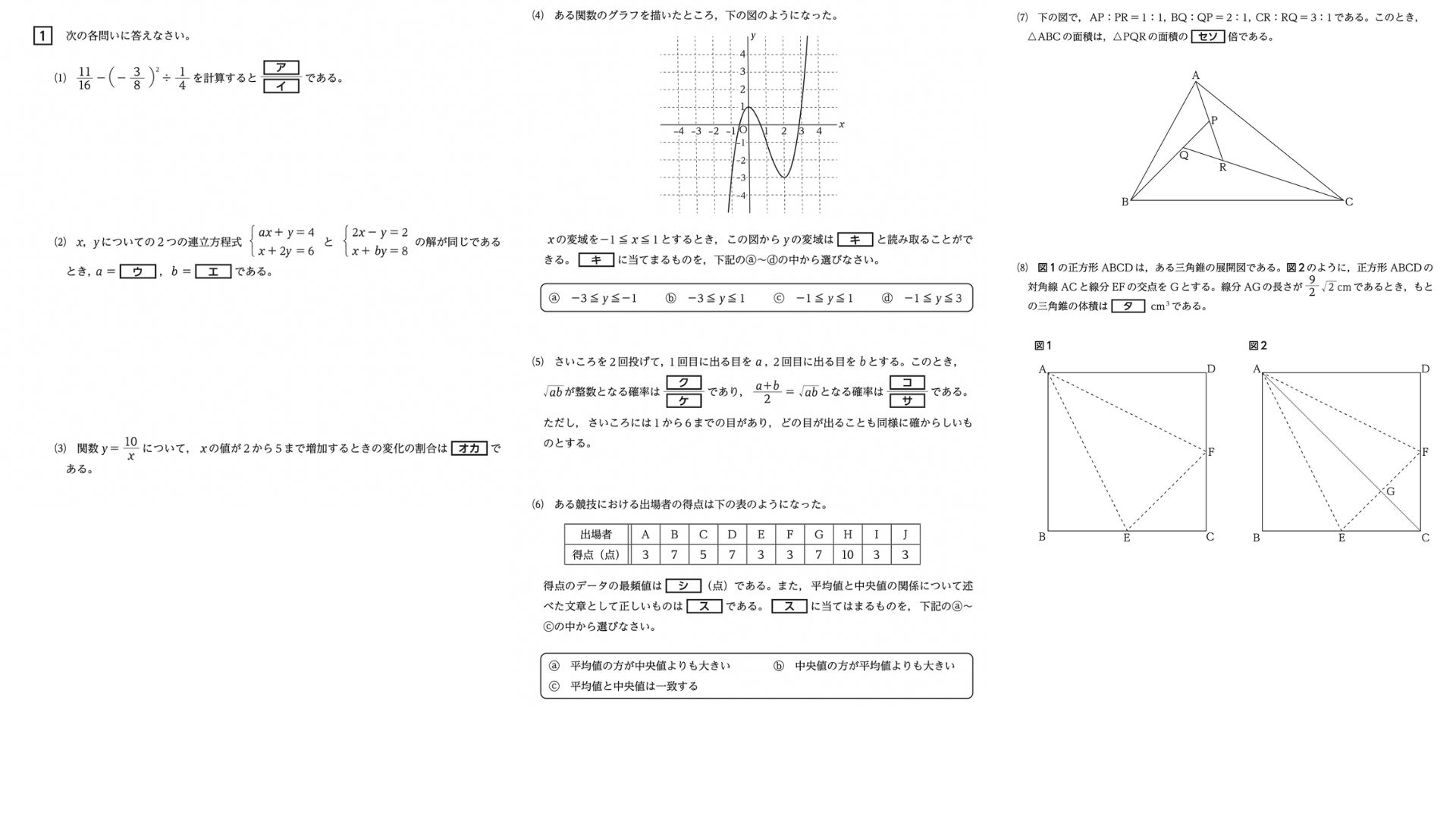
下記の令和7年度の高専過去問(本試験)を確認すると、
大問1の(1)~(6)は比較的難易度の低い計算問題となっており、
(7)、(8)が少し難易度の高い図形問題になっています!
比較的取りやすいからこそ、点数を落としたくありません!
ただ、解けない問題はありませんが、ここは10分で8問のペースで進めるのが理想です!!
そのためには、普段からの計算力の向上
さらに、解法を閃く力を養っておく必要性があります!
高専入試の数学で安定した点数を取りたい人はまずは大問1の満点化を目指していきましょう!
高専入試(数学)の出題傾向/関数
次に大問2〜4で出題される単元についてお話しいたします。
高専入試の数学は大問1~4で構成され、大問1で小問集合、大問2~4で関数、方程式、規則性、図形に関する問題から3パターンが出題されます。基本的に図形問題は必ず出題されるので、年によって、方程式・規則性・関数のうちから2題が出題されています。
その中で関数の問題ですが、主に2次関数の問題が多く出題されています。
過去5年での出題回数と出題内容は以下の通りです。
| 出題の有無 | 内容 | |
|---|---|---|
| 令和7年 | 出題あり(2次関数&反比例) | グラフと図形の面積の問題 |
| 令和6年 | 出題あり(2次関数&1次関数) | グラフと図形の長さの問題 |
| 令和5年 | 出題あり(2次関数&1次関数) | グラフと図形の面積の問題 |
| 令和4年 | 出題あり(2次関数&1次関数) | 動く図形の文章題 |
| 令和3年 | 出題あり(2次関数&1次関数) | 文章問題 |
このように直近5年間では全て出題されており、基本的にメインは2次関数になっています。
関数の問題は多くの出題パターンが作れますが、そのほとんどが
「座標を求める」
「関数の式を求める」
問題に落ち着きます!!
全ての問題において同じ解き方に見えるようにするためにも、問題を分解して解くクセをつけておく必要があるでしょう!
また、高専入試の数学の中では関数問題が小問集合の次に解きやすい問題であることが多いです!
関数の単元を苦手にしている人はしっかりと振り返るようにしていきましょう!!
高専入試(数学)の出題傾向/方程式
高専入試においてごく稀に方程式の問題が出題されます。
直近5年における方程式の出題状況は以下の通りです。
| 出題の有無 | 内容 | |
|---|---|---|
| 令和7年 | 出題なし | – |
| 令和6年 | 出題なし | – |
| 令和5年 | 出題あり(文章題) | 割合を用いた連立方程式 |
| 令和4年 | 出題なし | – |
| 令和3年 | 出題なし | – |
上記を見る限り、ここ5年間で1回しか出題されていないなら、対策しなくてもいいと思ったら大間違いです!!
なぜ、方程式の単元が出題されないかというと、それは関数も規則性の問題も考え方の根本が方程式であるため、
規則性か関数を出題しておけば、方程式の力も確認することができるのです!
逆に言うと、方程式とはそれほど重要な単元であるため、高専入試数学への対策だけでなく、数学を極めたいならまずは方程式を理解することから始めておきましょう!!
高専入試(数学)の出題傾向/図形
高専入試において図形問題は毎年必ず出題されます。
直近5年における図形単元の出題状況は以下の通りです。
| 出題の有無 | 内容 | |
|---|---|---|
| 令和7年 | 出題あり(平面図形) | 円における問題 |
| 令和6年 | 出題あり(平面図形) | 円における問題 |
| 令和5年 | 出題あり(空間図形) | 立体における問題 |
| 令和4年 | 出題あり(平面図形) | 円に関する問題 |
| 令和3年 | 出題あり(平面図形) | 図形の性質の利用 |
この図形問題の難易度が高専入試の数学において最も難しいといっても過言ではありません。
それはなぜかというと、
出題される問題が基本的に「中3単元の応用問題」になるからです!
例えば、
・相似の利用
・円周角の定理
・三平方の定理
など、公立中学校であれば、中3の10月ごろから習い始める単元を応用問題として出題してきます。
これらの図形問題を解こうとした場合、まず確実に予習を進めることが重要になってきます!
中学校と同じペースで進んでしまうと、基礎の理解までしか終わらず高専入試レベルの応用問題が全くできない。
という状態になります。
遅くても10月末までに中3単元を終わらせて、応用問題を見ていく・過去問対策を始めるくらいのペースでスケジュールを組みましょう!
また、これらの相似以降の単元を学習することでこれまでの問題のレベルがまた一段と向上します!
その時に意識しないといけないのは「何を求める時にその定理や方法、式を使うのかの整理」です!
必ずこの内容を意識しながら新たな単元を学習するように心がけましょう!
高専入試(数学)の出題傾向/規則性
高専入試において規則性の問題はよく出題されます。
直近5年における規則性問題の出題状況は以下の通りです。
| 出題の有無 | 内容 | |
|---|---|---|
| 令和7年 | 出題あり | プログラムに関する問題 |
| 令和6年 | 出題あり | 表を用いた問題 |
| 令和5年 | 出題なし | – |
| 令和4年 | 出題あり | プログラムに関する問題 |
| 令和3年 | 出題あり | 段を利用した問題 |
規則性の問題も出題頻度が高い問題になってきます!
規則性の問題で意識する点はどのような規則があり、その規則をどうすれば文字式で表すことができるのか?
ここを見つけることが重要です!
また、規則性の問題を解く上で気をつける点は、時間を意識しながら解くことです。
規則が見つかり、文字式・方程式が見つかるとすぐに解ける問題ですが、それが見つからない以上は必ずといっていいほど解けない問題になります。
時間とシビアになりながら、さまざまな問題パターンを通して、規則性問題を対策していく必要性があります。
高専合格への数学対策/最重要課題!

ここまで、高専入試の数学がどのような問題なのかを説明してきましたが、ここからが具体的に高専入試の数学に対してどのようにして対策していくべきなのかを説明いたします!!
高専合格への意識変革/①なんとなくを止める学習法を
まず高専入試に対して点数を取りたいなら、勉強方法を変えるしかない!!
というのが結論です!
どういうことかというと、定期テストのようにその期間だけ解き方を覚えて解けるようになるという勉強方法は入試には使えません…
なぜなら、入試というのは定期テストとは違い、中1~中3までの膨大な範囲での理解度が要求されるからです!
だからこそ、受験生がしないといけないのは「覚えているから解ける」という意識から「自分で導き出せる」という解き方に変える必要性があるのです!
全てを覚えきるのではなく、覚えてなくてもできる!
そのためには仕組みを理解するという意識が必要です!!!
例えば、小麦の生産量が世界で最も多い国は?という問題があるとします。
これを覚えておかないと解けないという状況は正直危ないです!!
だからこそ、なぜそうなるのか???という意識を考えていく必要性があるのです!
この場合、小麦の特性を考えてみるのです!
小麦はパンや麺などの主食として生産されます。
ここまで理解できれば、次は主食にはどのような特徴があるかを考えていきます。
10人家族の家庭と一人暮らしの家庭を想像してみてください。
主食となるお米の消費量を考えてみましょう!
その場合、10人家族の家庭の方が消費量が多いことが容易に想像がつきます!
すなわち、主食の生産量は人口にある程度依存することがわかります。
だからこそ、人口が多く、より多くの生産ができる広い面積を持っている国といえば、中国と考えられるのです!
この意識を持つだけで、自分自身が暗記している知識から推測して答えを当てられることができるようになります。
このようにただ単純な暗記内容でも必ずその根拠というものが存在します!
根拠をとらえて学習することが高専合格に向けて最も重要なことになってきます!
高専合格への意識変革/②応用力の向上に向けた学習法を
上記でも挙げている通り、正直全てを暗記して対策するは不可能に近いです!
その上で高専合格に対しては、どうしても応用問題を解かないといけない場面が存在します!
では、初見問題・応用問題に対して対応するためにどのような意識を持って取り組むべきかというと、
どのような問題パターンの時に特定の解法を使うのかをパターン化していく必要性があります!
より、パターン化意識するためには以下の手順で問題をみる・分析するクセをつける必要性があるのです!
①求めたい答えは何なのか?
→ここの意識が抜け始めると、途中で何をすればいいのかが分からないという現象が発生します!
②解きたい答えに対して、どのような方法・式で解くことができるかを想像する!
→求めたい答えが見えたらその答えを求めるためにどうするべきなのか。
ここに関しては、自分自身の知識との照らし合わせになります。
計算問で唯一覚えることがあるとしたらここになります。
③わかっている情報の整理を丁寧に行う。
→応用問題は何を持って応用問題というかというと、解き方が難しいのではなく、解かないといけない数量が多い(情報が不足している)からこそ応用問題として扱われます。
応用問題が解けない時は
・解き方を知らない
・何をすればいいか見えなくなる
のどちらかです!
解き方を知らない問題は覚えていけばいいので、重要な意識があるとすれば、
何をすればいいのか分からない問題をどう解いていくのかをより丁寧にみていくことが大切です!
書いてる情報を読み取るのはもちろん、書いてる情報から読み取れる(求められる)内容を全て可視化、理解しておくことが求められます。
④ここまで理解できたら、何が不足しているから解けないのかの原因を探る
応用問題が解けない最も大きな原因が解き方は想像できているが、不足している情報により、その解き方が使えないということになります。
だからこそ、③のわかっている情報をきちんと整理して、何が足りていないのかを自分自身が把握することが重要です!
ここまでわかれば、最後の手順です!
⑤解けない原因・不足している情報を求めるための解法を想像する!
ここまで考えてその方法が見えた時には、あとは今までの手順を逆算して答えを求めにいく形になります。
この時に解法を見つけるためにも、普段から何を求めるときにどのような方法があるのかを整理していく必要性があるのです!!
こうすることで、初見問題への対応力が上がるのと同時に、限られた時間の中で正解を導き出すという入試において最も重要な要素を育むことができるのです!!
入試は50分の中で問題を解ききる必要性が出てきます!
そうなると、どうしても問題に対する閃き力が求められます!
今、簡単に応用問題を解く方法を書かせていただきましたが、これを実際の問題を扱いながらより具体的に伝えているのが、
毎月1回実施している特別講座になります!!!
高専入試対策特別講座のメリットとは?

高専入試対策特別講座を受ける意味がどこにあるのか?
今回はそのメリットをお伝えいたします!!
高専入試対策特別講座のメリット①高専入試のゴールが知れる
高専入試対策特別講座では、前述の通り、高専の過去問を見ながら対策をしていきます!
高専の過去問に関しても、すでに習った単元の中から問題を出題させていただくため、自分自身が知っている単元をどれだけのレベル感で理解しておく必要性があるのかを体感することが可能です!
高専入試に対するゴールを明確にすることで、自分が「どのペース」で「何を重要視」しながら勉強していくべきなのかを体感できます!
それに伴い、高専入試に対するスケジュール感も捉えやすくなるでしょう!
高専入試対策特別講座のメリット②高専入試の対策法が見える
高専入試対策特別講座では、皆様の問題に対する意識を変化させます!
なぜなら皆様がこの1年間でするべき勉強はテスト勉強ではなく、受験勉強です!
2026年2月のタイミングでは、1~3年生のどの単元も等しく理解して解ける力を養う必要があります!
では、今のような勉強方法で大丈夫でしょうか??
覚え続ける勉強法、暗記していないと解けない問題…
そのような不安な状態で入試を迎えるのではなく、答えを自分で導き出せる考え方を作っておくべきです!
そうすることで、時間制限のある入試問題でも安定した点数を取ることができるのです。
ただ、この考え方は一朝一夕でどうにかなるようなものではありません。
だからこそ、この時期からコツコツと積み重ねていくしかないのです!
その新たな勉強方法をどのようなポイントを元に進めていくのか。
この内容を特別講座にて皆様にお伝えいたします!
飛高専塾の直近のイベントはこちら
高専模試
飛高専塾が実施している「高専模試」とは、
高専受験の経験がある講師陣が15年以上の過去問から問題傾向を分析した、限りになく高専入試の傾向に沿った模擬試験となっております。(予想問題を兼ねています。)
特に、難易度の高い数学や理科はもちろん、英語や社会においても、高専入試を突破する上で必要な知識を問う問題を作成しています。
国立高専を志望している中学生を対象とした模試となっており、
塾生以外も模試の受験は可能です。
また、全国各地の高専志望者に向けた、オンラインでの模試受験も可能となっています!
こちらは、中学3年生に向けた模試となっております!
下記にて直近で行われる中学3年生向けの高専模試の詳細をお知らせいたします!
| 詳細 | |
|---|---|
| 日程 | 2025年10月26日(日)〜2025年11月9日(日) |
| 申し込み締切 | 10月25日(土)22時まで |
| 参加方法 | 対面受講orオンライン受講を選択 |
| 参加費用 | 5,000円 |
| 内容 | 9:15~9:25までに集合(対面受講の場合) 9:30~10:20 理科 10:40~11:30 英語 11:50~12:40 数学 12:40~13:30 昼休憩 13:30~14:20 国語 14:40~15:30 社会 解散 |
| 実施場所(対面) | 飛高専塾 ・広島駅前校(広島県) (オンライン受講も可) |
| 持参物 | 筆記用具、腕時計、昼食、飲料 |
| 問い合わせ方法 | ・申し込みフォームから問い合わせ |
詳細につきましては、下記からご確認お願いいたします!
高専模試についてはこちら
高専模試について
高専模試の申し込みはこちら
高専模試に申し込む
高専入試特別講座

飛高専塾の特別講座では、これまで多くの受験生に対して「高専受験へのスタート」を実現させてきました!
高専入試のプロがする高専に「受かるにはここから始めよう!」
を高専過去問レベルで体験できる貴重なイベントです!
特別講座を受けるメリットは何か??
①問題に対する意識の変革が可能!
②高専入試に対して正しく危機感を持てる!
③高専合格に向けた最初の1歩を踏み出すことができる!
・「何をするべきか」
・「どうすれば高得点が狙えるのか」
・「問題への向き合い方の意識改革」
を徹底的に説明いたします!
※塾生以外の参加ももちろん可能となっています!
高専入試特別講座の詳細はこちら!
中3対象! 高専入試特別講座は以下の日程で実施いたします。
| 詳細 | |
|---|---|
| 日程 | 2025年10月19日(日)16時から18時 |
| 申し込み締切 | 10月18日(土)22時まで |
| 参加方法 | 対面受講orオンライン受講を選択 |
| 参加費用 | 無料 |
| 内容 | ○数学・英語の公開授業 ・高専入試に向けての問題の向き合い方 ・高専入試合格までの勉強スケジュールについて ・応用問題を解き切るための方法紹介 ・高専入試の問題を実際に演習 ・「数学で勝つ」ための解き方を伝授 |
| 実施場所(対面) | 飛高専塾 ・広島駅前校(広島県) (オンライン対応も可能です) |
| 持参物 | 筆記用具とノート、飲料 |
| 問い合わせ方法 | ・申し込みフォームから問い合わせ |
また、高専入試特別講座にご参加いただいた方全員に以下の特典を全てプレゼントいたします!
| 特典内容 |
|---|
・高専合格の無料判定面談の実施 ・必須連語・単語集(PDF)をプレゼント ・直近の高専模試の無料受験 ・高専受験に向けたロードマップをプレゼント ・高専合格に向けた学習計画の提示 ・過去問15年分(数・理・英)をプレゼント |
こちらの詳細は下記からご確認ください!
高専入試特別講座についてはこちら
高専入試特別講座について
高専入試特別講座の申し込みはこちら
高専入試特別講座に申し込む
高専入試説明会

高専を目指している中学生に向けて
高専入試のプロが何をするべきか対策法を徹底的に説明!
高専入試説明会はこんな人にオススメ
①高専に興味を持っていて適切な対策が知りたい人
②高専合格までの勉強量や、やるべきことをはっきりさせたい人

③高専受験へのモチベーションを上げたい人
④高専入試に不安を抱き高専の詳細が知りたい人
入試説明会は高専の受験を検討している
すべての中学生・保護者様が対象となっています。
※新中学1年生・新中学2年生も対象です。
高専を目指している中学生に向けて
高専入試のプロが高専入試に向けて何をするべきか徹底的に説明!
高専入試無料説明会の詳細はこちら!
第3回の高専入試無料説明会は以下の日程で実施いたします。
| 詳細 | |
|---|---|
| 日程 | 2025年10月18日(土)14時から15時 |
| 申し込み締切 | 10月17日(金)22時まで |
| 参加方法 | 対面受講orオンライン受講を選択 |
| 参加費用 | 無料 |
| 内容 | ・高専入試制度の紹介 ・高専入試に向けて今やるべき対策の紹介 ・合格するために目指すべき生徒像の紹介 ・高専合格に向けたロードマップの紹介 |
| 実施場所(対面) | 飛高専塾 ・広島(広島駅前本校) ・(オンラインも選択可能) |
| 持参物 | 筆記用具とメモ書類 |
| 問い合わせ方法 | ・公式ラインから問い合わせ ・申し込みフォームから問い合わせ |
また、入試説明会にご参加いただいた方全員に以下の特典を全てプレゼントいたします!
| 特典内容 |
|---|
| ・必須連語・単語集(PDF)をプレゼント ・直近の高専模試の無料受験 ・高専受験に向けたロードマップをプレゼント ・志望高専の合格判定を高専受験のプロが実施 ・高専合格に向けた学習計画の提示 ・過去問15年分(数・理・英)をプレゼント |
こちらの詳細は下記からご確認ください!
高専入試説明会についてはこちら
無料説明会について
高専入試説明会の申し込みはこちら
無料説明会を申し込む